How does comma work?
Lockdown probability matrices: Choosing which actions agents can do every day
The goal of this type of matrices is to specify what’s the likelihood of choosing a particular action, given the agents’ set of features.
We want to calculate the probability of action A, given a number \(N\) of binary features \(f_{i}\) of an agent.
To ensure that the probability is a number between 0 and 1, we use the sigmoid function
This function gives a value close to one for large \(x\), close to zero for large negative \(x\), and \(1/2\) for \(x=0\). \(x\) will depend of the features of the agent, and we can assing a weight \(\beta_{i}\) for each feature: A positive \(\beta\) means that the action is more probable to happen if the feature is present, a negative \(\beta\) that the action is less likely. We can write:
Where the \(f_{i}\) are the binarized (dummyfied/one-hot-encoded) features, that can take values 0 or 1. To see the effect of assigning different betas has on the probability, let’s look at the plot below, showing \(p_A\) as the function of the sum in imput to the sigmoid.
[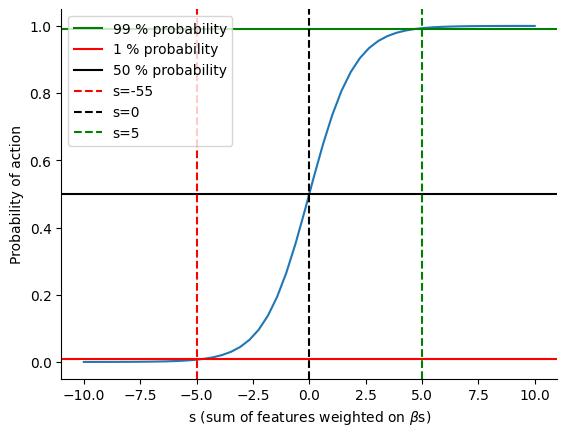 ]
]
If all betas are 0, the probability of A is 0.5.
When the sum of beta is roughly 5, the action is almost certain to happen (~99% probability)
When the sum of beta is ~ -5, the action is almost impossible (p<1%) This can help to assign the beta to each feature: a contribution of -5 means making the action almost impossible, + 5 certain. The user can think about betas as changes in the probability with respect to the 0.5 baseline. A different baseline can be added with it’s own beta: If the particular action has a \(\beta_{baseline}=-2\), for example, the action will have a probability of ~0.2, instead of 0.5, if all other features are not contributing.
Possible changes: - the scale of the sigmoid can be changed easily, so if it’s easier for the user to think in betas on the scale from-1 to 1 (x=1 making the action almost certain, x=-1 making it almost impossible), this can be easily tweaked. - The sigmoid does never output exactly 0 or exactly 1. While I think this is a good thing (real certainty never exists), one can introduce a threshold and say: \(p_{A}=0\) if \(x<th\), or \(p_{a}=1\) if \(x>th\), on top of the sigmoid shape.